What Is a Merkle Tree in Blockchain?

In the world of blockchain technology, where security and efficiency are paramount, data structures like Merkle Trees play a crucial role. If you’ve ever wondered how blockchains can verify massive amounts of transactions quickly without rechecking every single one, Merkle Trees are the unsung heroes behind that magic. Named after computer scientist Ralph Merkle, who patented the concept in 1979, a Merkle Tree is essentially a way to organize and summarize data using cryptography. It’s like a family tree for data hashes, allowing systems to confirm information integrity with minimal effort.

At its core, a Merkle Tree helps blockchain networks handle large datasets securely. Whether you’re dealing with cryptocurrency transactions, smart contracts, or decentralized apps, understanding Merkle Trees can give you deeper insights into how blockchains maintain trust and speed. In this article, we’ll break it down simply, explore how it works, and discuss its real-world applications.

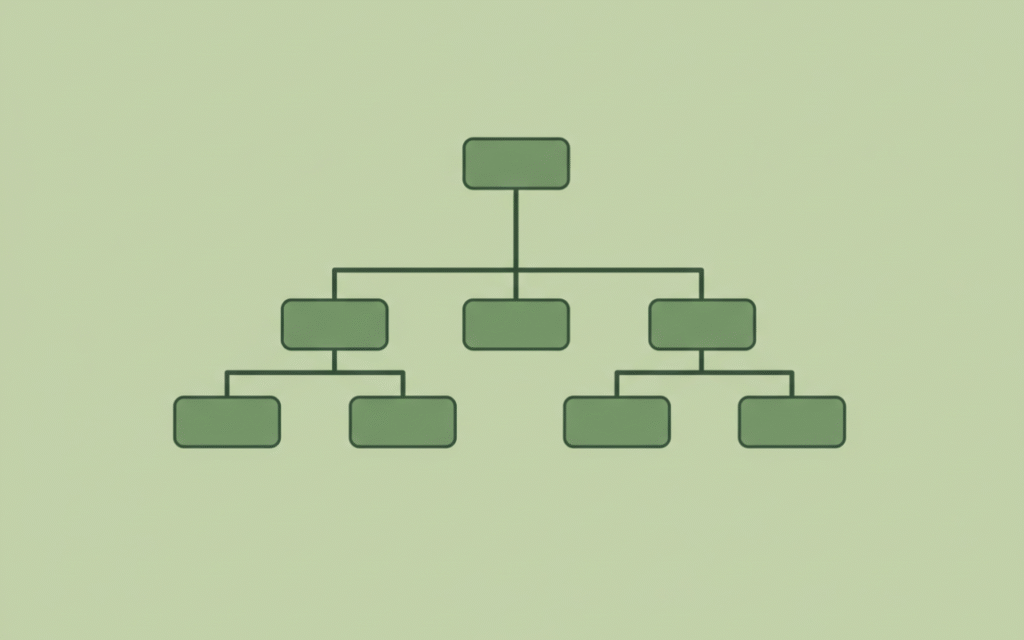
How Does a Merkle Tree Work?

To grasp a Merkle Tree, think of it as an upside-down tree: the “leaves” at the bottom represent individual pieces of data, and the “root” at the top is a single summary hash. Everything in between connects through hashing, which is a one-way mathematical function that turns data into a fixed-size string of characters (like a digital fingerprint).

➤ Step-by-Step Breakdown

1. Start with Data Blocks: Imagine you have four transactions in a blockchain block: A pays B $10, C pays D $20, E pays F $5, and G pays H $15. Each transaction is a “leaf” node.
2. Hash the Leaves: Apply a hash function (like SHA-256 in Bitcoin) to each transaction. This creates unique hashes: Hash A, Hash B, Hash C, and Hash D.
3. Pair and Hash Upward: Pair the leaf hashes and hash them together to form parent nodes. For example:
   • Hash of (Hash A + Hash B) = Hash AB
   • Hash of (Hash C + Hash D) = Hash CD
   If there’s an odd number of leaves, the last one might be duplicated or handled specially to keep the tree balanced.
4. Build Higher Levels: Repeat the process with the new parent hashes. Hash AB and Hash CD combine to form the Merkle Root: Hash of (Hash AB + Hash CD).

Why Are Merkle Trees Used in Blockchain?

Blockchains are distributed ledgers, meaning every participant (node) needs to agree on the data’s validity. Without efficient tools, verifying thousands of transactions per block would be slow and resource-intensive. Here’s where Merkle Trees shine:

➢ Efficiency in Verification

In a full blockchain node, you don’t need to store or check every transaction to confirm one. A light client (like a mobile wallet) can request a Merkle Proof for a specific transaction. By hashing along the provided path and matching the known root (stored in the block header), it verifies authenticity in logarithmic time super fast even for huge trees.

For instance, in Bitcoin, each block header includes the Merkle Root. This lets Simplified Payment Verification (SPV) clients check transactions without downloading the entire blockchain, saving bandwidth and storage.

➢ Enhanced Security

Merkle Trees ensure data integrity. Since hashes are cryptographic and collision-resistant (hard to find two inputs with the same output), any alteration is immediately noticeable. This is vital for preventing fraud in decentralized systems where no central authority oversees everything.

➢ Scalability Benefits

As blockchains grow (think Ethereum with millions of daily transactions), Merkle Trees help scale by enabling sharding dividing the network into smaller parts while still allowing cross-verification. They’re also key in state proofs for layer-2 solutions like rollups, where off-chain computations are summarized on-chain.

Real-World Examples of Merkle Trees

• Bitcoin: Every block uses a Merkle Tree to summarize transactions. Miners compute the root during block creation, and nodes use it for quick validations.
• Ethereum: Employs Merkle Patricia Tries (a variant combining Merkle Trees with prefix trees) for storing account states, transactions, and receipts. This supports efficient queries in smart contracts.
• Other Uses: Beyond blockchain, Merkle Trees appear in Git for version control (tracking file changes) and certificate transparency logs for secure web browsing.

If you’re building a blockchain app, libraries like Python’s merkletools or JavaScript’s merkletreejs make implementing them straightforward. Start by hashing your data arrays and recursively building the tree, test with small datasets to see the proofs in action.

Advantages and Limitations

➡ Pros

• Speed: Verification is O(log n) complexity, ideal for large-scale systems.
• Space Savings: Only paths need sharing, not full data.
• Privacy: Prove data existence without exposing details.

➡ Cons

• Complexity in Implementation: Building and maintaining balanced trees requires careful coding to avoid vulnerabilities.
• Dependency on Hash Functions: If a hash algorithm is broken (unlikely with modern ones like SHA-3), the tree’s security weakens.
• Not for All Data Types: Best for static datasets, dynamic ones might need variants like Merkle DAGs (Directed Acyclic Graphs) used in IPFS.

➟ To mitigate limitations, always use battle-tested hash functions and audit your code.

FAQ

What is the difference between a Merkle Tree and a binary tree?

A binary tree is a general structure where each node has up to two children. A Merkle Tree is a specific type of binary tree where nodes store hashes, enabling cryptographic proofs of data inclusion and integrity.

Can Merkle Trees be used outside of blockchain?

Yes! They’re valuable in any system needing efficient data verification, like distributed file systems (e.g., IPFS), version control (Git), or even auditing logs in databases.

How do I create a simple Merkle Tree?

In Python, install merkletools via pip, then: Import it, add leaf hashes, build the tree, and get proofs. Experiment with sample transactions to understand the root calculation.

Are Merkle Trees secure against quantum attacks?

Current hash functions like SHA-256 are vulnerable to future quantum computers. Post-quantum alternatives like hash-based signatures are being developed to future-proof them.

Why is it called a “tree”?

It resembles a tree structure in nature, branches (internal nodes) leading to a trunk (root), with leaves as the base data points. This hierarchical design allows efficient navigation from root to leaf.